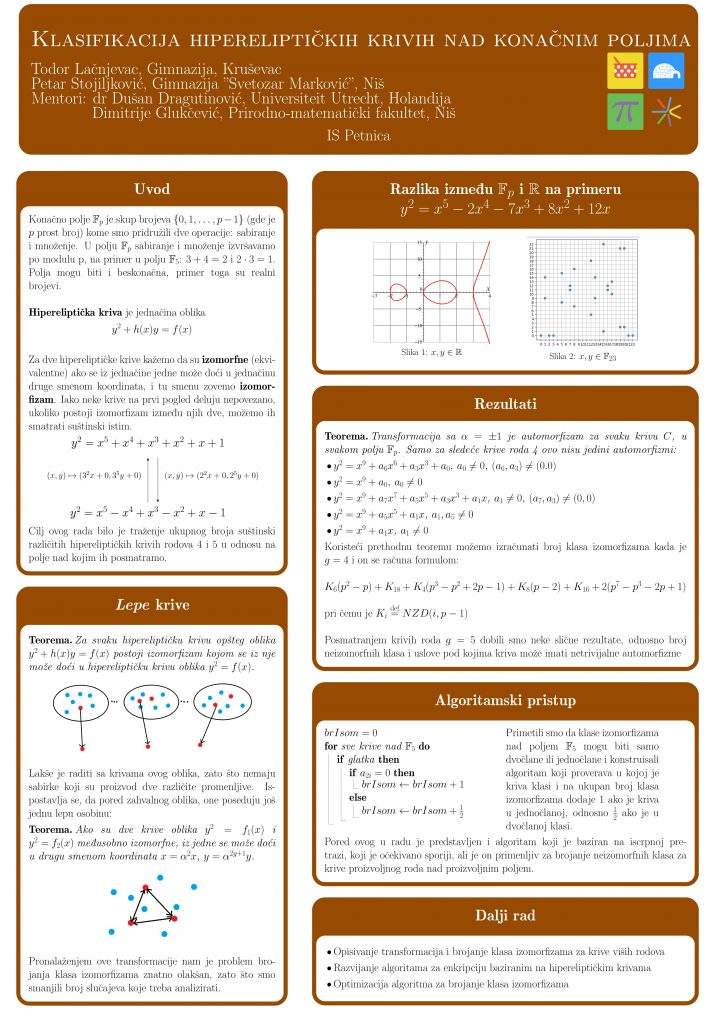
Klasifikacija hipereliptičkih krivih nad konačnim poljima
Lačnjevac Todor, 3. razred, Gimnazija, Kruševac
Stojiljković Petar, 4. razred, Gimnazija ”Svetozar Marković”, Niš
Mentori:
dr Dušan Dragutinović, Universiteit Utrecht, Holandija
Dimitrije Glukčević, Prirodno-matematički fakultet, Niš
Hipereliptičke krive roda najviše 3 nad konačnim poljima proučavaju se i preporučuju za primenu u kriptografiji već oko dve decenije. Iako se krive viših rodova generalno ne smatraju dovoljno bezbednim za klasične kriptografske primene poput digitalnog potpisa, određene specijalne krive ovog roda mogu imati prednosti u kontekstu sistema zasnovanih na sparivanju. Klasifikacija hipereliptičkih krivih po izomorfizmu igra ključnu ulogu u izboru bezbednih krivih za praktične primene. Dok su klase izomorfizama za krive roda 2 i 3 već detaljno proučene, ovaj rad se bavi računanjem broja klasa izomorfizama kod hipereliptičkih krivih rodova 4 i 5 nad konačnim poljima karakteristike veće od tri. Pored toga, analizirani su uslovi pod kojima takve krive poseduju netrivijalne automorfizme. U radu su predstavljena i dva algoritma za brojanje klasa: jedan baziran na iscrpnoj pretrazi, a drugi efikasniji, koji koristi neke osobine krivih pri fiksiranju polja nad kojim su posmatrane.
Skupovi malog broja skretanja
Đurić Nađa, 4. razred, Valjevska gimnazija, Valjevo
Kragulj Marko, 3. razred, Deveta gimnazija „Mihailo Petrović Alas”, Beograd
Mentori:
Veljko Toljić, Prirodno- matematički fakultet, Novi Sad
Aleksa Džuklevski, Faculty of Mathematics and Physics, Charles University, Prague
Skup je najviše k-skrećući ako za svake dve tačke A i B postoji izlomljena linija sa k skretanja koja spaja A i B i cela se nalazi u skupu, gde izlomljenu liniju definišemo kao niz duži A1B1, A2B2, …AkBk, tako da važi Bi=Ai+1. Kažemo da je neki skup k- skrećući ako je k najmanji ceo broj skretanja tako da je skup najviše k- skrećući. U ovom radu bavimo se svojstvima konveksnih skupova koja se lepo mogu generalizovati za skupove malog broja skretanja; ili idealno, za svako k∈ N0. Fokusirali smo se na k- skrećuće mnogouglove. U ovom radu dokazano je da su svi mnogougovi čija se svaka dva maksimalna konveksna podskupa seku 1- skrećući. Pored ovoga, određen je i broj skretanja komplementa 1- skrećućih mnogouglova, ali i da za k>1 ne postoji gornja granica broja skretanja komplementa. Takođe je pokušana generalizacija Hejlijeve teoreme za k- skrećuće mnogouglove, i pokazano je da teorema ne važi za k- skrećuće mnogouglove u dve i tri dimenzije.
Promešani antikvadrati (Shuffle Anti-squares)
Nikolić Pavle, 3. razred, Gimnazija Ćuprija
Mentor:
Bašić Bojan, Prirodno-matematički fakultet, Novi Sad
Kombinatorika na rečima je oblast koja se bavi analiziranjem nizova simbola i nalazi primenu u mnogim oblastima gde se oni pojavljuju, kao što su kriptografija i analiza DNK sekvenci. Navedene nizove nazivamo rečima. Osnovni pojam podoblasti kojom se bavimo je posebna vrsta reči koje se nazivaju promešani kvadrati. Promešani kvadrat je reč koja se može rastaviti na dve disjunktne identične podreči, pri čemu podreč podrazumeva reč koja se može dobiti brisanjem slova iz početne reči. U radu „Variations on shuffle squares“, Grytczuk et al. postavljaju hipotezu da, za svaku parnu dužinu 2n za n>12, postoji tzv. promešani antikvadrat dužine 2n; pritom, pojam promešanog antikvadrata se definiše kao reč takva da, donekle neformalno govoreći, nijedna reč koja se može dobiti kao ciklični pomeraj posmatrane reči nije promešani kvadrat. U ovom radu je navedena hipoteza dokazana. Dokaz je konstruktivne prirode. Najpre je kompjuterskom analizom manjih primera uočena klasa reči određenog opšteg oblika za koju je delovalo verovatno da reči proizvoljno velike dužine iz te klase jesu promešani antikvadrati, a potom je ova tvrdnja i dokazana detaljnom strukturnom analizom posmatrane klase reči (bez oslanjanja na kompjuterska ispitivanja).